Teichmüller Theory Volume 3: Manifolds that Fiber over the Circle

Teichmüller Theory

and Applications to Geometry, Topology, and Dynamics

Volume 3: Manifolds that Fiber over the Circle

by John H. Hubbard

ISBN 9781943863013
Hardcover, 558 pages
241 color illustrations

Introduction
Table of contents
Index
Sample pages

Also see Volume 1: Teichmüller Theory
Volume 2: Surface Homeomorphisms and Rational Functions

I’ve just finished reading your 3-volume Teichmuller theory book. It’s a masterpiece. It’s one of the best math books I’ve ever read, and reading it was sheer pleasure. It’s one of my favorite subjects, and on every topic I thought your coverage was exactly right. -- Professor Danny Calegari, University of Chicago

This book shows that a 3-manifold that fibers over the circle has a hyperbolic structure if and only if the holonomy of the fibering is pseudo-Anosov. Proving this result requires a lot of background.

The first chapter concerns hyperbolic geometry and Kleinian groups. Topics include Jørgensen's inequality, the Margulis lemma, algebraic and especially geometric limits with both the Chabauty and the Thurston-Gromov approaches, the Klein-Maskit combination theorems, the Poincaré polyhedron theorem, and geometrically finite Kleinian groups.

The second chapter covers rigidity theorems: Ahlfors, McMullen, and Mostow. Verifying that quasi-Fuchsian groups satisfy the hypothesis of the McMullen rigidity theorem is a long and beautiful trip through laminations and pleated surfaces.

The third chapter proves the main result, visiting on the way the compactness of Bers slices, R-trees, Chiswell functions, Hatcher's construction and Skora's theorem, and the Otal compactness theorem.

The appendices take up 200 pages. Topics include the Nullstellensatz and Selberg's lemma, the relation between the ideal class group and the ends of Bianchi manifolds, the Haudorff dimension (1) of the space of simple geodesics on a hyperbolic surface, period coordinates, the ergodic theorem and Hopf's argument, the volume of strata of quadratic differentials, a minimal measured foliation that is not ergodic, and the Thurston norm and its relation to hyperbolic structures.

You will find a brief introduction to Chapters 11-13 below, along with a sampling of illustrations.

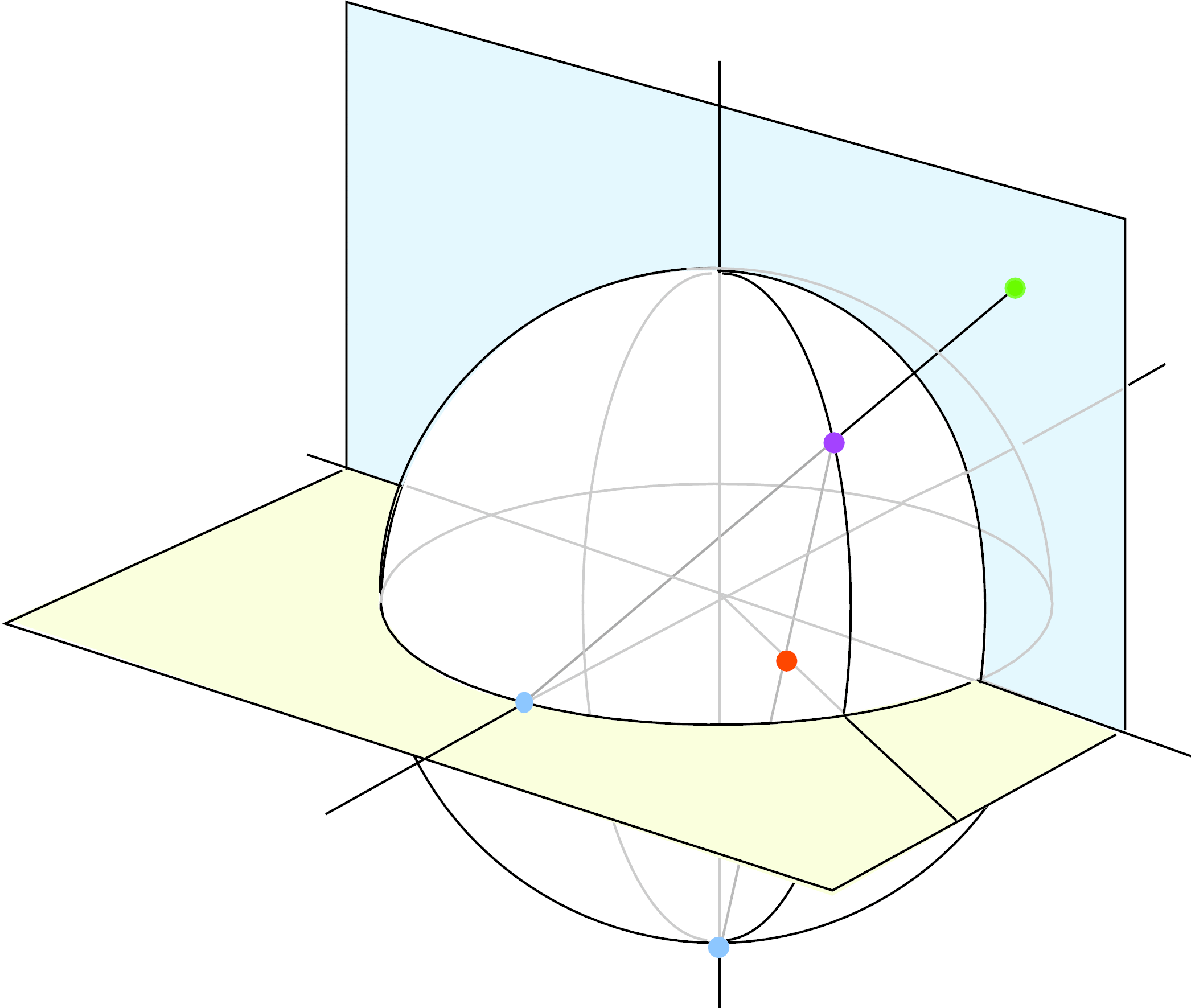
Chapter 11 Geometry of hyperbolic space

This chapter gives a short introduction to the geometry of hyperbolic space and to Kleinian groups. We begin in Sections 11.1-11.4 with hyperbolic space and its group of automorphisms. Section 11.5 treats elementary and non-elementary Kleinian groups. Section 11.6 defines the limit set of a Kleinian group and gives some of its basic properties.

Section 11.7 explores the Jørgensen inequality, a beautiful and rather mysterious inequality that exploits the discreteness of a Kleinian group in an essential way. This leads in Section 11.8 to a fairly easy proof of the Margulis lemma, which gives a complete description of the thin parts of a hyperbolic 3-manifold. It is a 3-dimensional analogue of the collaring theorem (Theorem 3.8.3) and extends the plumbing picture of hyperbolic surfaces given in Section 3.8.

I find the proof of Jørgensen's inequality hard to motivate, so I also give in Appendix D2 a different proof of the Margulis lemma, which is cruder, but much more natural (and which generalizes to higher dimensions).

Thurston's hyperbolization theorems require not just thinking about individual Kleinian groups, but also thinking about their limits. There are two notions of ``limit of a sequence of Kleinian groups'', with surprisingly different properties: algebraic limits, which are relatively easy to understand, and geometric limits, which can be amazingly complicated. Algebraic limits are described in Section 11.9, geometric limits in Section 11.10. In particular, we show that the Chabauty description and the Thurston-Gromov description of the geometric topology coincide.

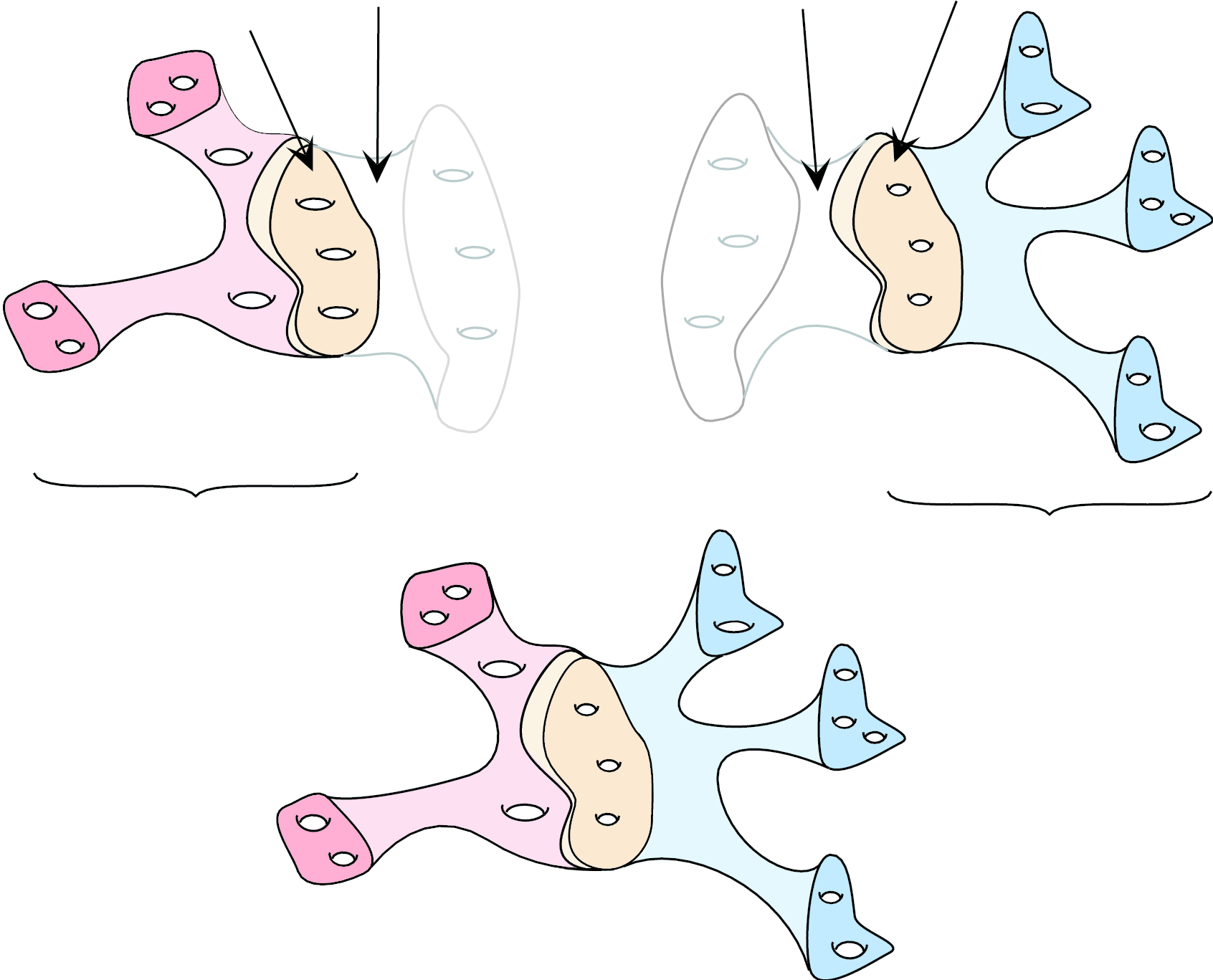
Thurston's second hyper-bolization theorem requires the Klein-Maskit combination theorems, which will eventually allow us to glue together hyperbolic mani-folds. These theorems, proved in Section 11.11, also illustrate the power of 3-dimensional thinking about Kleinian groups; it is quite hard to see why the combined groups as defined are discrete if one sticks to the action on the Riemann sphere.

In Section 11.12, we prove the 3-dimensional analogue of the Poincaré polygon theorem. I also discuss examples of Kleinian groups, including the hyperbolic structure of the complement of the figure-eight knot and its relationship to Bianchi groups. Finally, Section 11.13 defines geometrically finite Kleinian groups. These are the groups that are classified by points of appropriate Teichmüller spaces, leading in due course to the skinning lemma in Volume 4.

(Click here to see the first four pages of Chapter 11, in pdf)

Chapter 12 Rigidity theorems

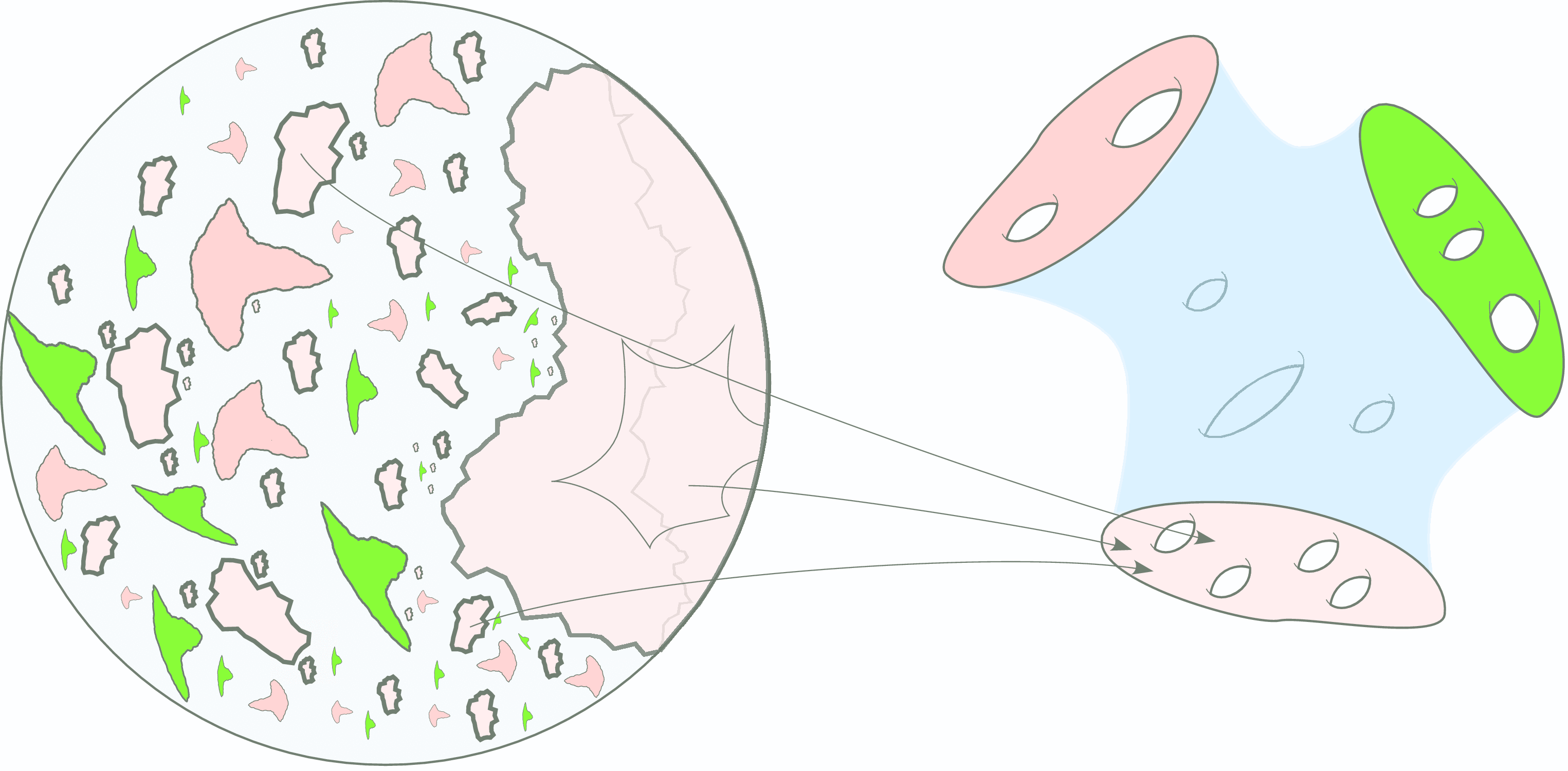
In the first half of this chapter we prove three great theorems, due to Ahlfors, McMullen, and Mostow. Although the statements look quite different, they are technically closely related: they are all concerned with the construction of Beltrami forms invariant under a Kleinian group. Since these theorems show that such Beltrami forms are very restricted, they are called rigidity theorems

In the second half of the chapter we prove that the central hypothesis of McMullen's rigidity theorem holds for quasi-Fuchsian groups. We need this to prove the hyperbolization theorem for 3-manifolds that fiber over the circle. Along the way we develop several topics, including laminations and pleated surfaces, of great interest in their own right.

(Click here to see the first four pages of Chapter 12, in pdf)

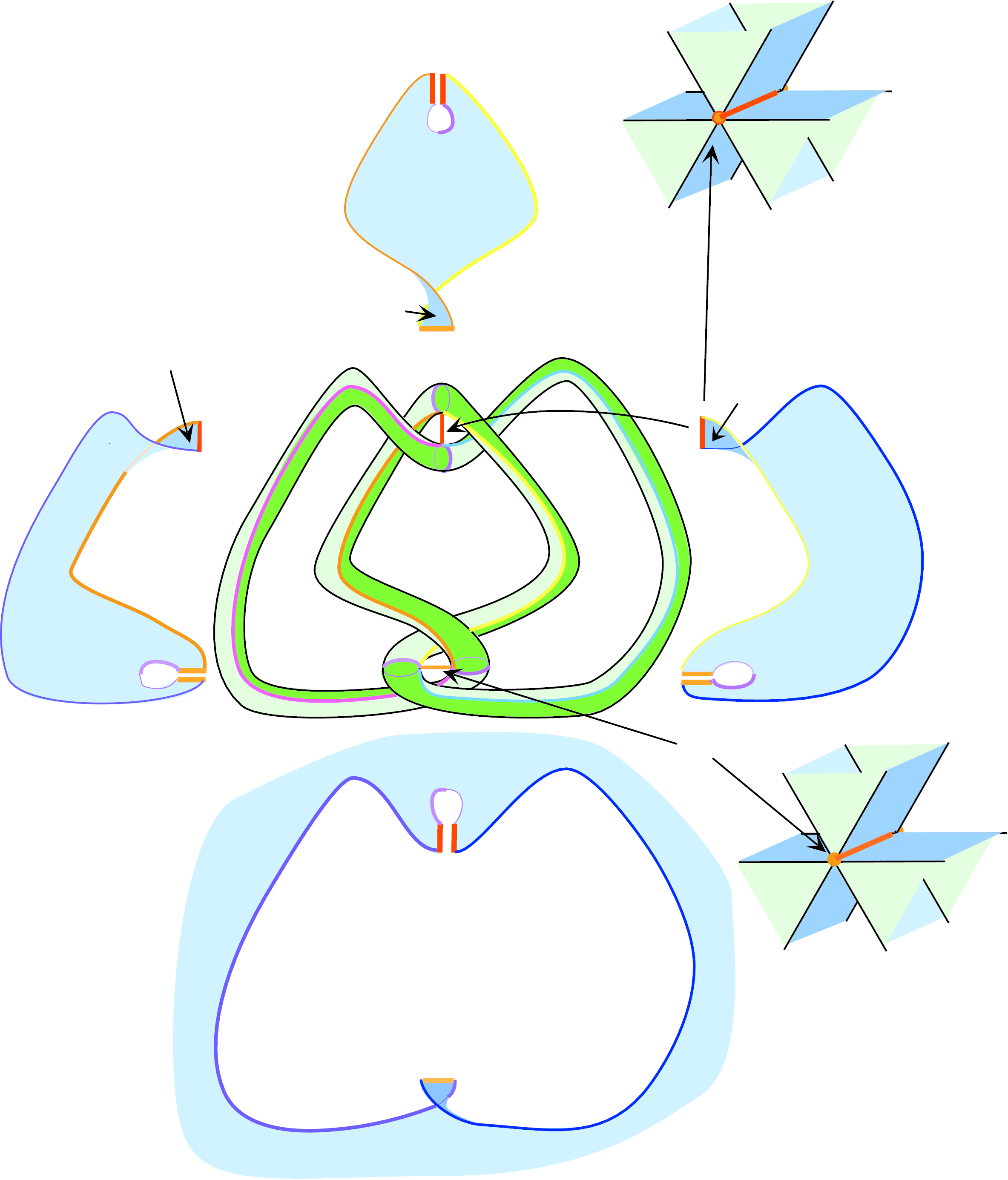
Chapter 13 Hyperbolization of 3-manifolds that fiber over the circle

One of the great accomplishments of nineteenth century mathematics was showing that all surfaces of genus at least 2 admit hyperbolic structures. We now present a 3-dimensional version of this theorem: Theorem 13.0.1. This is one of the great accomplishments of twentieth century mathematics.

Let S be a compact surface with finitely many points removed, and let f be an orientation-pre-serving homeomorphism of S. Denote by M_f the mapping torus of f , i.e., the quotient of [0,1] x S by the equivalence relation that identifies (0, x) to (1, f(x)). Every 3-manifold that fibers over the circle is of this form; the corresponding map f is called the holonomy map. It is defined only up to isotopy and so is really an element of the mapping class group MCG(S).

Theorem 13.0.1 (Hyperbolization of 3-manifolds that fiber over the circle) The 3-manifold M_f admits a complete hyperbolic structure if and only if the holonomy map f is homotopic to a pseudo-Anosov homeomorphism.

Proving this theorem will take the entire chapter.

(Click here to see the first four pages of Chapter 13, in pdf)

Appendices

Clicking on the links below will take you to the first two pages of each appendix, in pdf.

Appendix D1 The Nullstellensatz and Selberg's lemma
Appendix D2 The Margulis lemma: another proof
Appendix D3 Fundamental groups, amalgamated sums, and HNN extensions
Appendix D4 Arithmetic Kleinian groups
Appendix D5 Ends of a topological space
Appendix D6 The space of simple geodesics
Appendix D7 Period coordinates
Appendix D8 Ergodic flow, Hopf's argument, and Mostow rigidity
Appendix D9 Teichmüller flow is ergodic
Appendix D10 Minimal but not ergodic
Appendix D11 Sullivan's rigidity theorem
Appendix D12 Fibrations and the Thurston norm