Future Books

Teichmüller Theory

and Applications to Geometry, Topology, and Dynamics

Volume 4: Hyperbolization of Haken Manifolds

by John H. Hubbard

Would you like to be notified when this book is published?

Volume 4 presents greater mathematical difficulties than the previous volumes, and we hesitate to hazard a publication date. Here we give the opening paragraphs of each chapter, as they now stand, and some figures. In the book, labels are included in the figures, using "puts". The placing of figures here does not reflect their placement in the book.

Chapter 14 Hierarchies in 3-manifolds

discs lowered and raised Proving Thurston's hyperbolization for Haken 3-manifolds will require three major tools: the existence of hierarchies in Haken manifolds, allowing us to cut a Haken manifold into polyhedra; Andreev's theorem, allowing us to give these polyhedra hyperbolic structures; and the skinning lemma, allowing us to glue the pieces together again. The first is topological, the second geometric, the third analytic.

This chapter proves the existence of hierarchies. It is much influenced by Allen Hatcher's notes on 3-manifolds [11] and by books by John Hempel [12] and William Jaco [13].

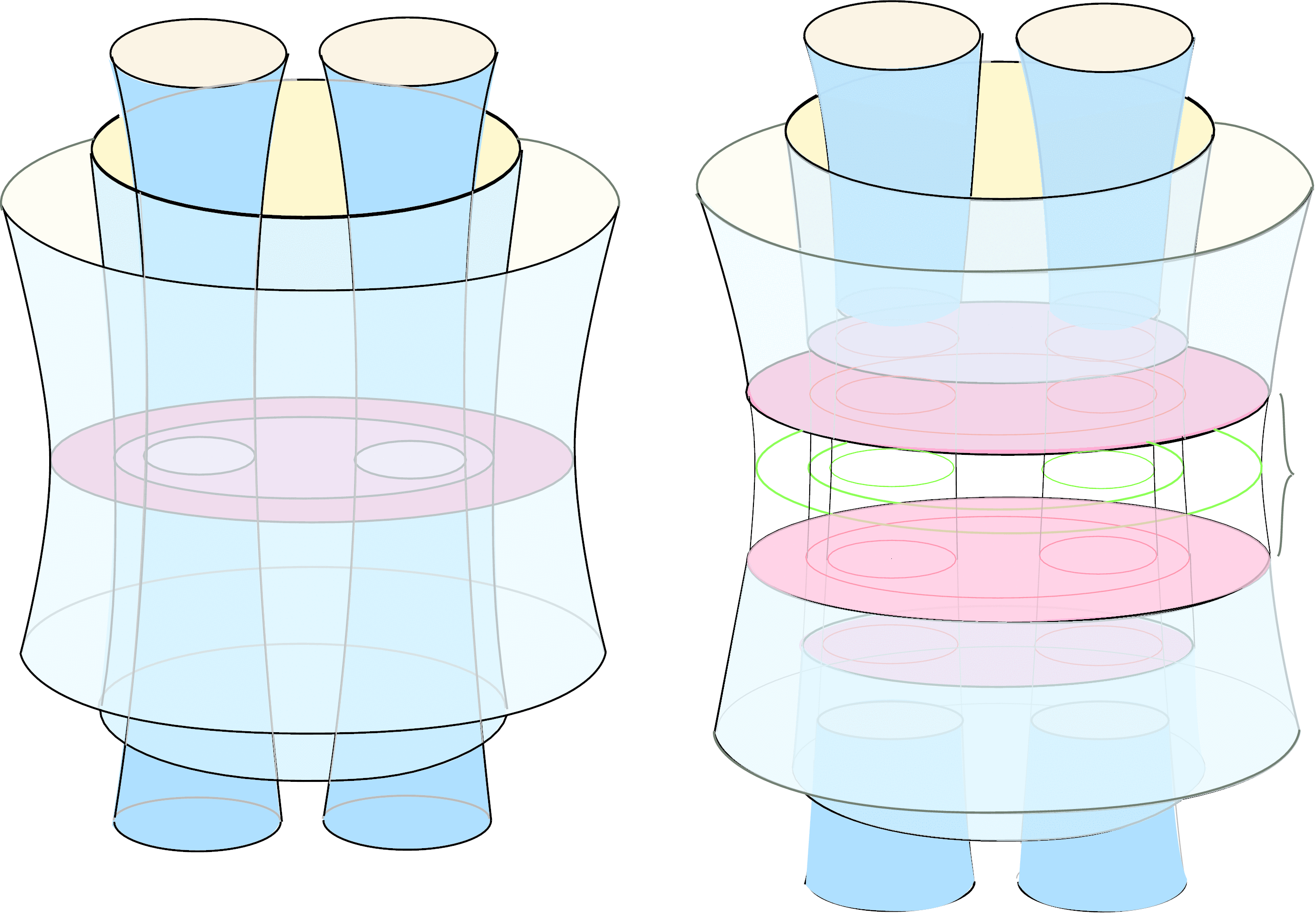
A hierarchy is a way to cut up a manifold along incompressible surfaces so that the resulting components are all homeomorphic to balls. To simplify the exposition, we will assume, unless otherwise specified, that all surfaces and 3-manifolds are connected, compact, and orientable. Their boundaries may be nonempty or they may be empty (in which case the manifolds are said to be "closed'': a closed manifold is compact without boundary).

Chapter 15 Andreev's theorem

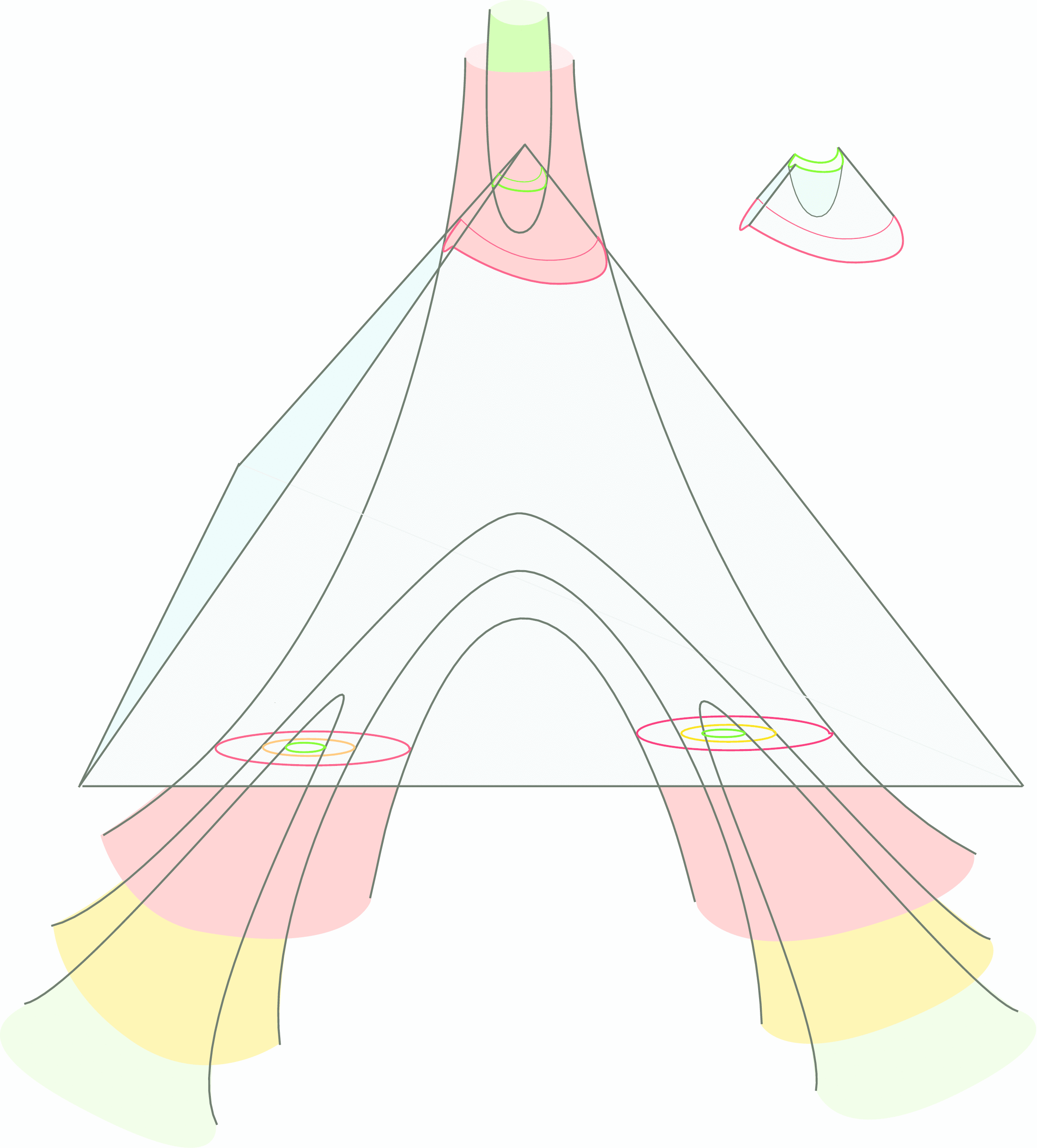
Here we present a beautiful theorem of Andreev [4], which provides a complete characterization of compact hyperbolic polyhedra with non-obtuse dihedral angles. The theorem is essential for proving Thurston's hyperbolization theorem for Haken 3-manifolds (Chapter 16).

Andreev's theorem (Theorem 15.2.4) says that if we make a topological model for a polyhedron, choosing candidate dihedral angles (angles between the faces) that are at most p/2, then there exist simply verifiable conditions that tell us whether a hyperbolic polyhedron with the assigned angles exists. Moreover, if such a polyhedron exists, it is unique.

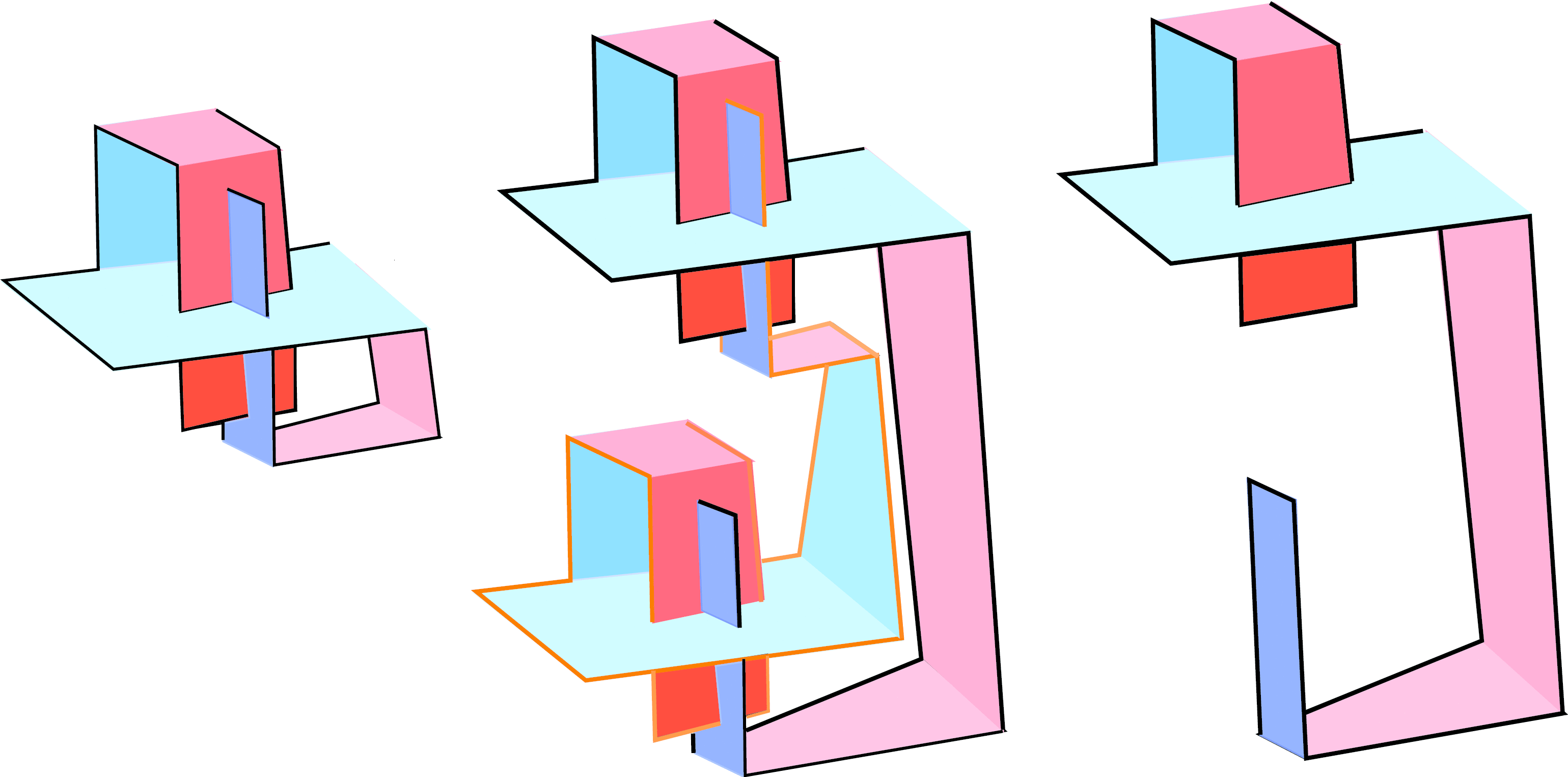Chapter 16 Hyperbolization of Haken manifolds

In Chapter 14 (Proposition 14.6.2) we showed that a Haken manifold M can be cut up into polyhedra (depending on how the cutting is done, we may end up with a single polyhedron or several). In Chapter 15 (Proposition 15.10.2) we showed that these polyhedra, perhaps after further subdivision, can be given hyperbolic structures with all dihedral angles right angles. In this chapter we will glue the polyhedra back together (perhaps gluing a face of one polyhedron to another face of the same polyhedron) to give M a hyperbolic structure.

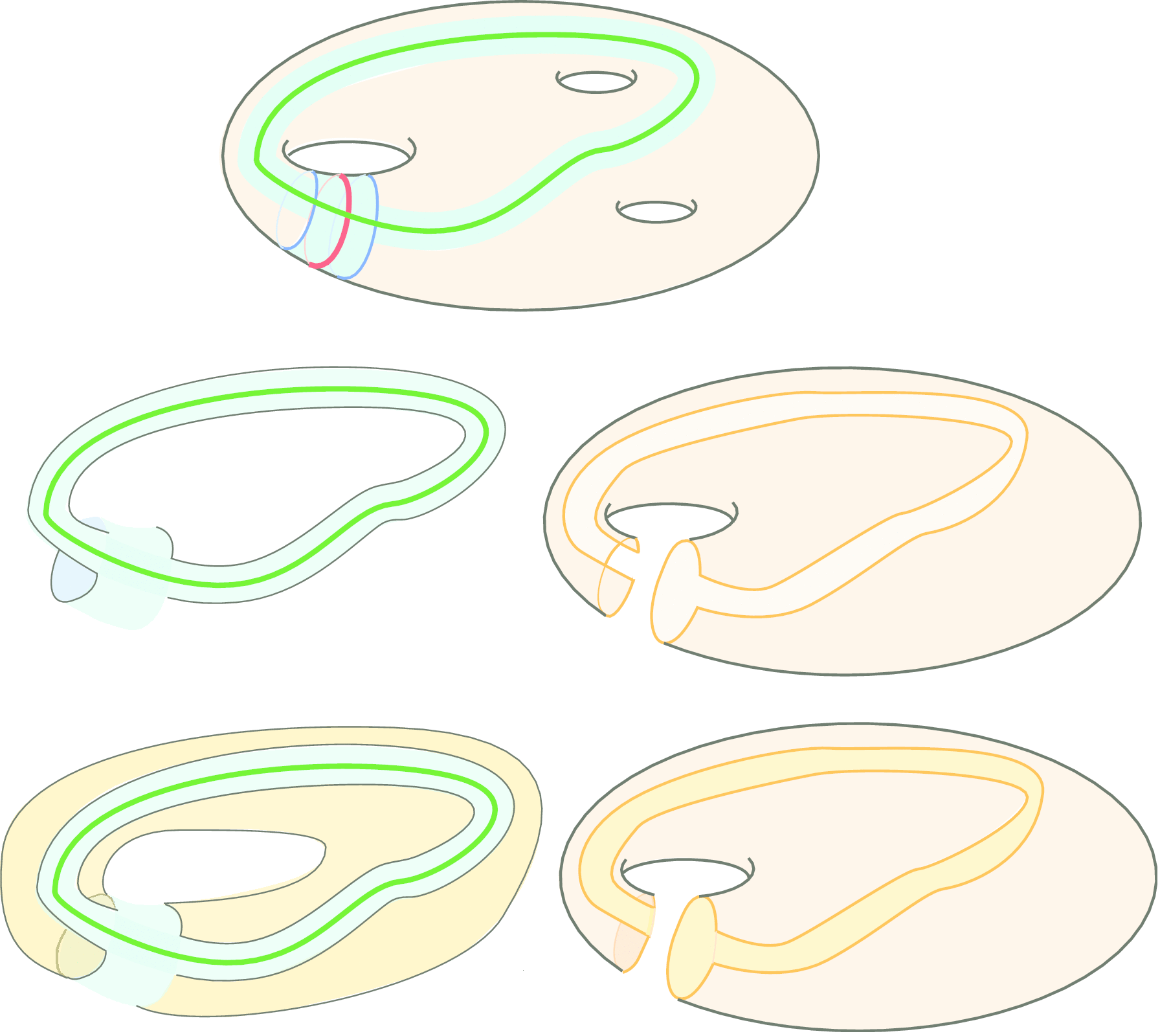
One dimension lower, you might think of cutting up a surface along a maximal multicurve, to produce trousers. Then give the individual trousers a hyperbolic structure.

You will only be able to sew the trousers back together if corresponding boundary components have the same length; fortunately Theorem 3.5.8 in Volume 1 guarantees that by choosing the hyperbolic structure appropriately, we can adjust these lengths any way we like. If we choose corresponding lengths to be equal, and then choose gluing maps, we arrive at the Fenchel-Nielsen description of hyperbolic structures on surfaces. Similarly, unless we are very careful, the faces of the polyhedra to be glued won't fit....