Teichmüller Theory

and Applications to Geometry, Topology, and Dynamics

Volume 2: Surface Homeomorphisms and Rational Functions

by John H. Hubbard

ISBN: 978-1-943863-00-6
262 pages, hardcover, smythe-sewn binding
108 color illustrations

2016, $84

Index (in pdf)
Table of contents (in html)
Sample pages (html)


Volume 1: Teichmüller theory
Volume 3: Manifolds that Fiber over the Circle
Volume 4: Hyperbolization of Haken Manifolds (not yet published)

---

I’ve just finished reading your 3-volume Teichmuller theory book. It’s a masterpiece. It’s one of the best math books I’ve ever read, and reading it was sheer pleasure. It’s one of my favorite subjects, and on every topic I thought your coverage was exactly right. -- Professor Danny Calegari, University of Chicago

---

From the introduction by the author:

This volume is the second of four volumes devoted to Teichmüller theory and its applications to geometry, topology, and dynamics. The first volume gave an introduction to Teichmüller theory.

Volumes 2 through 4 prove four theorems by William Thurston:

1. The classification of homeo-morphisms of surfaces
2. The topological characterization of rational maps
3. The hyperbolization theorem for 3-manifolds that fiber over the circle
4. The hyperbolization theorem for Haken 3-manifolds

These theorems are of extraordinary beauty in themselves, and the methods Thurston used to prove them were so novel and displayed such amazing geometric insight that to this day they have barely entered the accepted methods of mathematicians in the field.

The results sound more or less unrelated, but they are linked by a common thread: each one goes from topology to geometry. Each says that either a topological problem has a natural geometry, or there is an understandable obstruction.

The proofs are closely related: you use the topology to set up an analytic mapping from a Teichmüller space to itself; the geometry arises from a fixed point of this mapping. Thurston proceeds to show that if there is no fixed point, then some system of simple closed curves is an obstruction to finding a solution.

These theorems have been quite difficult to approach, in part because Thurston never published complete proofs of any of them.

In this second volume, in Chapters 8 and 10, I prove the first two of these theorems. Both proofs use most of the contents of Volume 1.

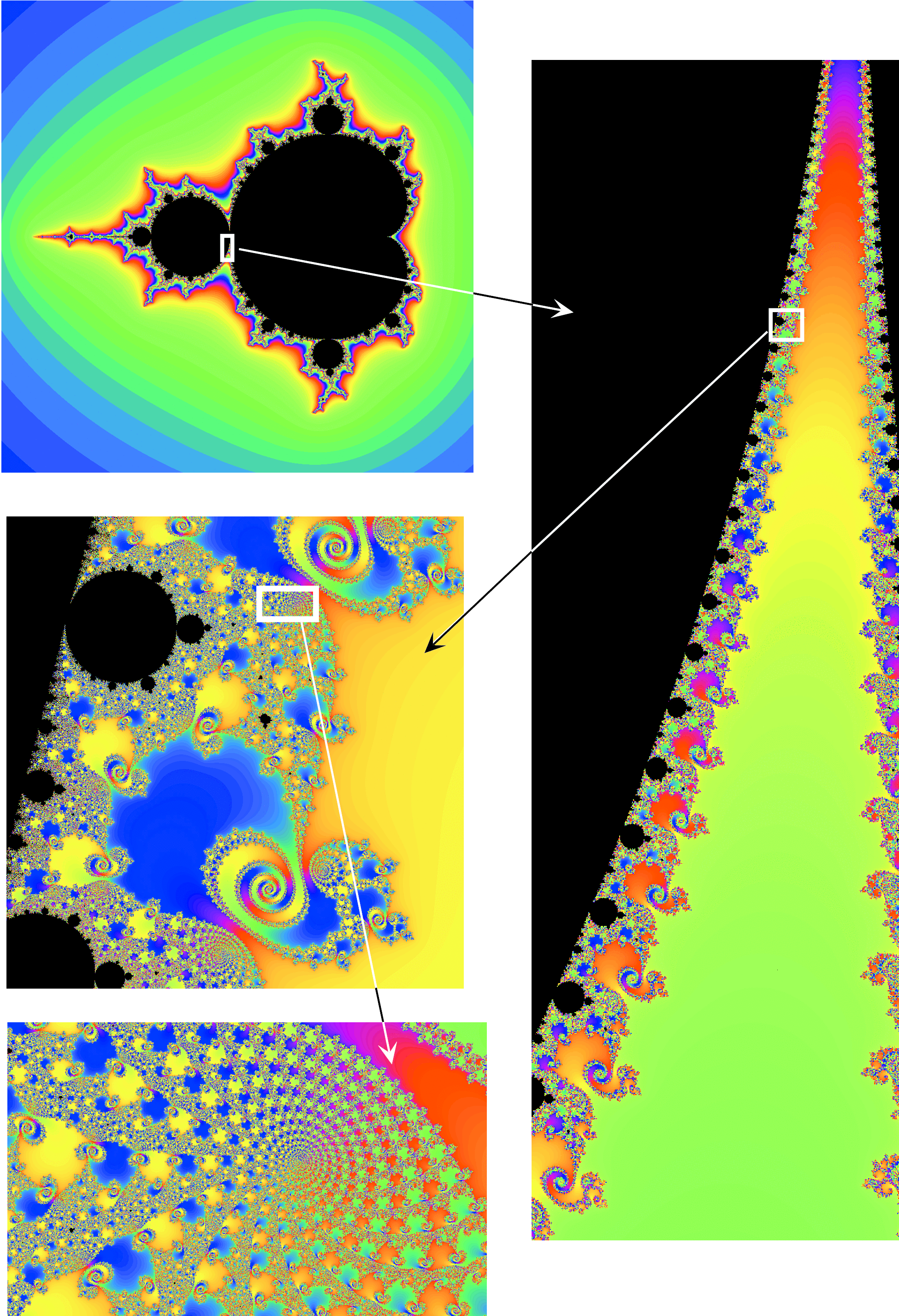
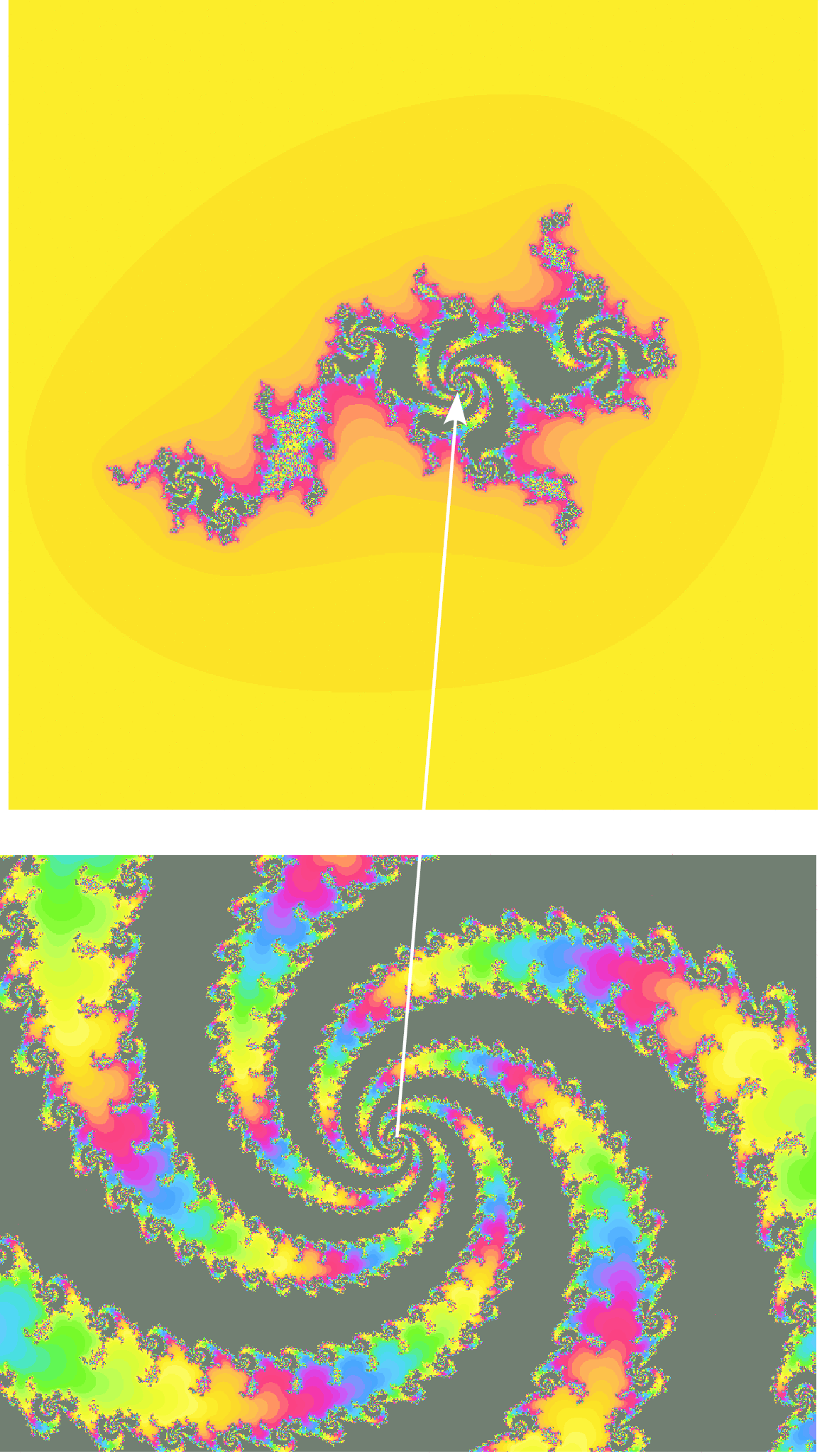
Chapters 8 and 10 also contain an extensive collection of examples. In Chapter 8 we exhibit some constructions of pseudo-Anosov mappings; Chapter 10 describes spiders and uses them to analyze the structure of the Mandelbrot set.

This requires the basics of dynamics in one complex variable; Chapter 9 contains the necessary material.

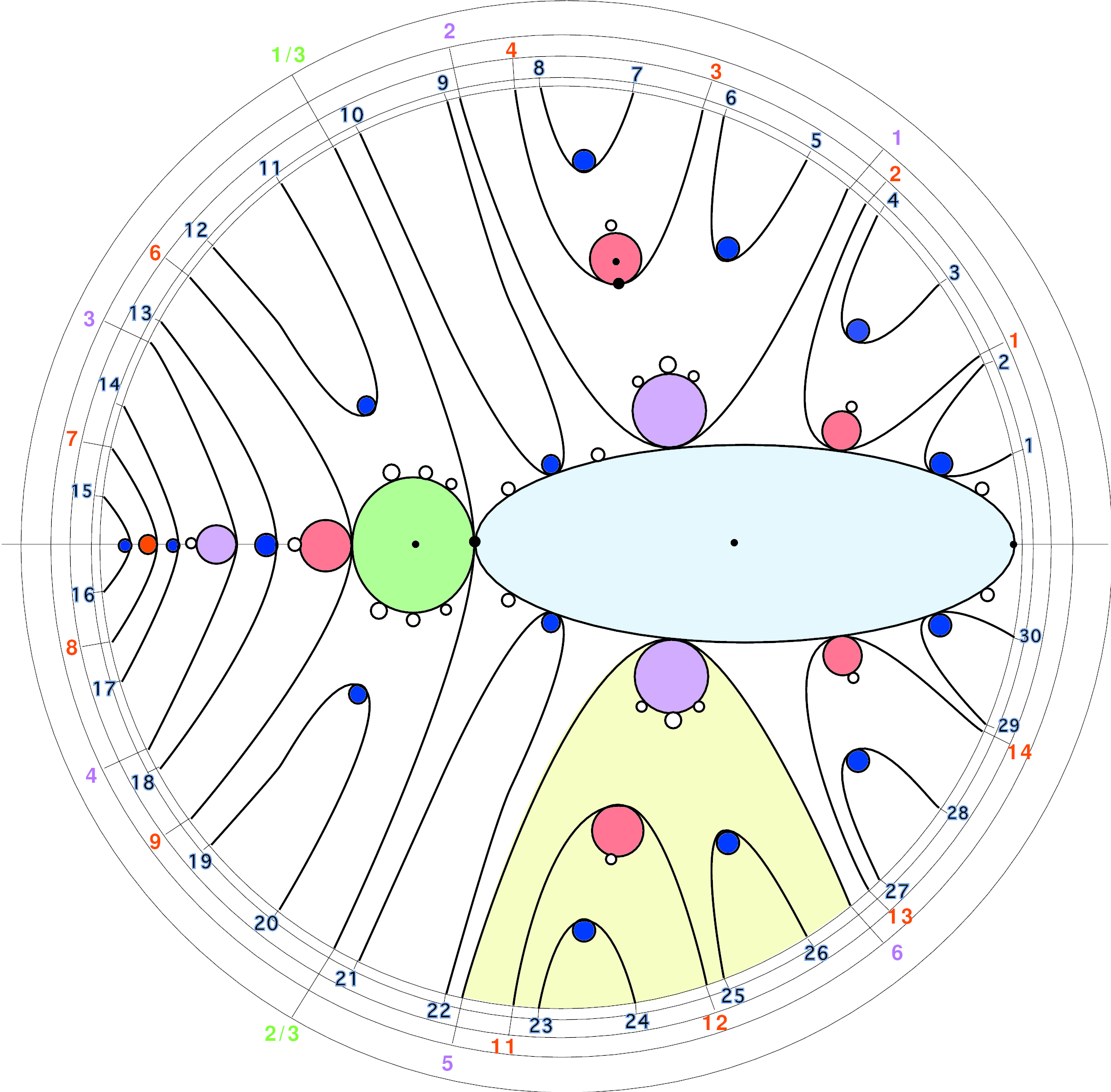
There are nine appendices. The first proves the Perron-Frobenius theorem; the next three treat some technical issues concerning the topology of surfaces and their homeomorphisms: the Alexander trick, homotopies and isotopies for surfaces, the algebraic definition of the mapping class group, and a list of generators for the mapping class group.

Appendix C5 outlines a recent result of Ursula Hamenstadt saying that "most'' stretch factors of pseudo-Anosov homeomorphisms are totally real.

Appendix C6 gives a bare bones treatment of irrationally indifferent fixed points to complete the cases treated in Chapter 9. It isn't really relevant to this book, but it is of such importance to complex dynamics that it seems a good idea to include it.

Appendices C7 and C8 are relevant to Chapter 10. Appendix C7 gives some examples of Thurston pullback maps. Appendix C8completes the main theorem by an analysis of postcritically finite branched maps with nonhyperbolic orbifolds.

Appendix C9 gives an introduction to Sullivan's dictionary, which pairs statements about 1-dimensional complex dynamics and statements about 3-dimensional hyperbolic geometry. Several topics are relevant to this volume, but the appendix is really about the relations of these topics to those that will be treated in Volumes 3 and 4.